The probability of improbable events. The simplicity amongst complexity. The purity in its best form. The ultimate cure for those who trade, for those who invest. Does it exist? Can we compute it? Is it really something impossible? In this post we challenge ourselves to the frontiers of accessible statistics and data analysis in order to find most optimal computable solutions to this enigmatic but mind-draining problem. Since there is no certainty, everything remains shrouded in the veil of probability. The probability we have to face and hope that something unlikely, determined to take place anyhow, eventually will not happen.
Our goal is to calculate the probability of a very rare event (e.g. a heavy and/or extreme loss) in the trading market (e.g. of a stock plummeting 5% or much more) in a specified time-horizon (e.g. on the next day, in one week, in one month, etc.). The probability. Not the certainty of that event.
In this Part 1, first, we look at the tail of an asset return distribution and compress our knowledge on Value-at-Risk (VaR) to extract the essence required to understand why VaR-stuff is not the best card in our deck. Next, we move to a classical Bayes’ theorem which helps us to derive a conditional probability of a rare event given… yep, another event that (hypothetically) will take place. Eventually, in Part 2, we will hit the bull between its eyes with an advanced concept taken from the Bayesian approach to statistics and map, in real-time, for any return-series its loss probabilities. Again, the probabilities, not certainties.
1. VaR (not) for Rare Events
In the framework of VaR we take into consideration $T$ days of trading history of an asset. Next, we drive a number (VaR) that describes a loss that is likely to take place with the probability of approximately $\alpha$. “To take place” does not mean here that it will take place. In this approach we try to provide some likelihood (a quantitative measure) of the rare event in a specified time-horizon (e.g. on the next day if daily return-series are under our VaR investigation; a scenario considered in this post).
If by $L$ we denote a loss (in percent) an asset can experience on the next day, then:
$$
\mbox{Pr}(L \le -\mbox{VaR}_{1-\alpha}) = \alpha
$$ would be the probability of a loss of $-L\times D$ dollars where $-L\times D\ge -\mbox{VaR}\times D$, equal, for instance, $\alpha=0.05$ (also referred to as $(1-\alpha)$% VaR measure; $\mbox{VaR}_{95}$, etc.) and $D$ is the position size (money invested in the asset in terms of physical currency, e.g. in dollars). In other words, the historical data can help us to find $\mbox{VaR}_{95}$ given $\alpha$ assuming 5% of chances that $\mbox{VaR}_{1-\alpha}$ will be exceeded on the next day.
In order to illustrate that case and its shortcomings when it comes to the analysis of rare events, let’s look at the 10 year trading history of two stocks in the NASDAQ market: highly volatile CAAS (China Automotive Systems, Inc.; of the market capital of 247M) and highly liquid AAPL (Apple Inc.; of the market capital of 750B). First, we fetch their adjusted close price-series from Yahoo! Finance and derive the corresponding daily return-series utilising Python:
# Predicting Heavy and Extreme Losses in Real-Time for Portfolio Holders
# (c) 2015 QuantAtRisk.com, by Pawel Lachowicz
#
# heavy1.py
import pandas.io.data as web
import matplotlib.pyplot as plt
import numpy as np
from pyvar import findvar, findalpha
# ---1. Data Processing
# fetch and download daily adjusted-close price series for CAAS
# and AAPL stocks using Yahoo! Finance public data provider
caas = web.DataReader("CAAS", data_source='yahoo',
start='2005-05-13', end='2015-05-13')['Adj Close']
aapl = web.DataReader("AAPL", data_source='yahoo',
start='2005-05-13', end='2015-05-13')['Adj Close']
CAAScp = np.array(caas.values)
AAPLcp = np.array(aapl.values)
f = file("data1.dat","wb")
np.save(f, CAAScp)
np.save(f, AAPLcp)
f.close()
# read in the data from a file
f = file("data1.dat","rb")
CAAScp = np.load(f)
AAPLcp = np.load(f)
f.close()
# compute return-series
retCAAS = CAAScp[1:]/CAAScp[:-1]-1
retAAPL = AAPLcp[1:]/AAPLcp[:-1]-1
The best way to understand the data is by plotting them:
# plotting (figure #1)
# adjusted-close price-series
fig, ax1 = plt.subplots(figsize=(10, 6))
plt.xlabel("Trading days 13/05/2005-13/05/2015")
plt.plot(CAAScp, '-r', label="CAAS")
plt.axis("tight")
plt.legend(loc=(0.02, 0.8))
plt.ylabel("CAAS Adj Close Price (US$)")
ax2 = ax1.twinx()
plt.plot(AAPLcp, '-', label="AAPL")
plt.legend(loc=(0.02, 0.9))
plt.axis("tight")
plt.ylabel("AAPL Adj Close Price (US$)")
# plotting (figure #2)
# daily return-series
plt.figure(num=2, figsize=(10, 6))
plt.subplot(211)
plt.grid(True)
plt.plot(retCAAS, '-r', label="CAAS")
plt.axis("tight")
plt.ylim([-0.25,0.5])
plt.legend(loc="upper right")
plt.ylabel("CAAS daily returns")
plt.subplot(212)
plt.grid(True)
plt.plot(retAAPL, '-', label="AAPL")
plt.legend(loc="upper right")
plt.axis("tight")
plt.ylim([-0.25,0.5])
plt.ylabel("AAPL daily returns")
plt.xlabel("Trading days 13/05/2005-13/05/2015")
We obtain the price-series

and return-series

respectively. For the latter plot, by fixing the scaling of both $y$-axes we immediately gain an chance to inspect the number of daily trades closing with heavy losses. Well, at least at first glance and for both directions of trading. In this post we will be considering the long positions only.
Having our data pre-processed we may implement two different strategies to make use of the VaR framework in order to work out the probabilities for tail events. The first one is based on setting $\alpha$ level and finding $-VaR_{1-\alpha}$. Let’s assume $\alpha=0.01$, then the following piece of code
# ---2. Compuation of VaR given alpha alpha = 0.01 VaR_CAAS, bardata1 = findvar(retCAAS, alpha=alpha, nbins=200) VaR_AAPL, bardata2 = findvar(retAAPL, alpha=alpha, nbins=100) cl = 100.*(1-alpha)
aims at computation of the corresponding numbers making use of the function:
def findvar(ret, alpha=0.05, nbins=100):
# Function computes the empirical Value-at-Risk (VaR) for return-series
# (ret) defined as NumPy 1D array, given alpha
# (c) 2015 QuantAtRisk.com, by Pawel Lachowicz
#
# compute a normalised histogram (\int H(x)dx = 1)
# nbins: number of bins used (recommended nbins>50)
hist, bins = np.histogram(ret, bins=nbins, density=True)
wd = np.diff(bins)
# cumulative sum from -inf to +inf
cumsum = np.cumsum(hist * wd)
# find an area of H(x) for computing VaR
crit = cumsum[cumsum <= alpha]
n = len(crit)
# (1-alpha)VaR
VaR = bins[n]
# supplementary data of the bar plot
bardata = hist, n, wd
return VaR, bardata
Here, we create the histogram with a specified number of bins and $-VaR_{1-\alpha}$ is found in an empirical manner. For many reasons this approach is much better than fitting the Normal Distribution to the data and finding VaR based on the integration of that continuous function. It is a well-know fact that such function would underestimate the probabilities in far tail of the return distribution. And the game is all about capturing what is going out there, right?
The results of computation we display as follows:
print("%g%% VaR (CAAS) = %.2f%%" % (cl, VaR_CAAS*100.))
print("%g%% VaR (AAPL) = %.2f%%\n" % (cl, VaR_AAPL*100.))
i.e.
99% VaR (CAAS) = -9.19% 99% VaR (AAPL) = -5.83%
In order to gain a good feeling of those numbers we display the left-tails of both return distributions
# plotting (figure #3)
# histograms of daily returns; H(x)
#
plt.figure(num=3, figsize=(10, 6))
c = (.7,.7,.7) # grey color (RGB)
#
# CAAS
ax = plt.subplot(211)
hist1, bins1 = np.histogram(retCAAS, bins=200, density=False)
widths = np.diff(bins1)
b = plt.bar(bins1[:-1], hist1, widths, color=c, edgecolor="k", label="CAAS")
plt.legend(loc=(0.02, 0.8))
#
# mark in red all histogram values where int_{-infty}^{VaR} H(x)dx = alpha
hn, nb, _ = bardata1
for i in range(nb):
b[i].set_color('r')
b[i].set_edgecolor('k')
plt.xlim([-0.25, 0])
plt.ylim([0, 50])
#
# AAPL
ax2 = plt.subplot(212)
hist2, bins2 = np.histogram(retAAPL, bins=100, density=False)
widths = np.diff(bins2)
b = plt.bar(bins2[:-1], hist2, widths, color=c, edgecolor="k", label="AAPL")
plt.legend(loc=(0.02, 0.8))
#
# mark in red all histogram bars where int_{-infty}^{VaR} H(x)dx = alpha
hn, nb, wd = bardata2
for i in range(nb):
b[i].set_color('r')
b[i].set_edgecolor('k')
plt.xlim([-0.25, 0])
plt.ylim([0, 50])
plt.xlabel("Stock Returns (left tail only)")
plt.show()
where we mark our $\alpha=$1% regions in red:

As you may notice, so far, we haven’t done much new. A classical textbook example coded in Python. However, the last figure reveals the main players of the game. For instance, there is only 1 event of a daily loss larger than 15% for AAPL while CAAS experienced 4 heavy losses. Much higher 99% VaR for CAAS takes into account those 4 historical events and put more weight on 1-day VaR as estimated in our calculation.
Imagine now that we monitor all those tail extreme/rare events day by day. It’s not too difficult to notice (based on the inspection of Figure #2) that in case of AAPL, the stock recorded its first serious loss of $L \lt -10$% approximately 650 days since the beginning of our “monitoring” which commenced on May 13, 2005. In contrast, CAAS was much more volatile and you needed to wait only ca. 100 days to record the loss of the same magnitude.
If something did not happen, e.g. $L \lt -10$%, the VaR-like measure is highly inadequate measure of probabilities for rare events. Once the event took place, the estimation of VaR changes (is updated) but decreases in time until a new rare event occurs. Let’s illustrate it with Python. This is our second VaR strategy: finding $\alpha$ given the threshold for rare events. We write a simple function that does the job for us:
def findalpha(ret, thr=1, nbins=100):
# Function computes the probablity P(X<thr)=alpha given threshold
# level (thr) and return-series (NumPy 1D array). X denotes the
# returns as a rv and nbins is number of bins used for histogram
# (c) 2015 QuantAtRisk.com, by Pawel Lachowicz
#
# compute normalised histogram (\int H(x)dx=1)
hist, bins = np.histogram(ret, bins=nbins, density=True)
# compute a default histogram
hist1, bins1 = np.histogram(ret, bins=nbins, density=False)
wd = np.diff(bins1)
x = np.where(bins1 < thr)
y = np.where(hist1 != 0)
z = list(set(x[0]).intersection(set(y[0])))
crit = np.cumsum(hist[z]*wd[z])
# find alpha
try:
alpha = crit[-1]
except Exception as e:
alpha = 0
# count number of events falling into (-inft, thr] intervals
nevents = np.sum(hist1[z])
return alpha, nevents
We call it in our main program:
# ---3. Computation of alpha, given the threshold for rare events
thr = -0.10
alpha1, ne1 = findalpha(retCAAS, thr=thr, nbins=200)
alpha2, ne2 = findalpha(retAAPL, thr=thr, nbins=200)
print("CAAS:")
print(" Pr( L < %.2f%% ) = %.2f%%" % (thr*100., alpha1*100.))
print(" %g historical event(s)" % ne1)
print("AAPL:")
print(" Pr( L < %.2f%% ) = %.2f%%" % (thr*100., alpha2*100.))
print(" %g historical event(s)" % ne2)
what returns the following results:
CAAS: Pr( L < -10.00% ) = 0.76% 19 historical event(s) AAPL: Pr( L < -10.00% ) = 0.12% 3 historical event(s)
And that’s great however all these numbers are given as a summary of 10 years of analysed data (May 13/2005 to May/13 2015 in our case). The final picture could be better understood if we could dynamically track in time the changes of both probabilities and the number of rare events. We achieve it by the following not-state-of-the-art code:
# ---4. Mapping alphas for Rare Events
alphas = []
nevents = []
for t in range(1,len(retCAAS)-1):
data = retCAAS[0:t]
alpha, ne = findalpha(data, thr=thr, nbins=500)
alphas.append(alpha)
nevents.append(ne)
alphas2 = []
nevents2 = []
for t in range(1,len(retAAPL)-1):
data = retAAPL[0:t]
alpha, ne = findalpha(data, thr=thr, nbins=500)
alphas2.append(alpha)
nevents2.append(ne)
# plotting (figure #4)
# running probability for rare events
#
plt.figure(num=4, figsize=(10, 6))
ax1 = plt.subplot(211)
plt.plot(np.array(alphas)*100., 'r')
plt.plot(np.array(alphas2)*100.)
plt.ylabel("Pr( L < %.2f%% ) [%%]" % (thr*100.))
plt.axis('tight')
ax2 = plt.subplot(212)
plt.plot(np.array(nevents), 'r', label="CAAS")
plt.plot(np.array(nevents2), label="AAPL")
plt.ylabel("# of Events with L < %.2f%%" % (thr*100.))
plt.axis('tight')
plt.legend(loc="upper left")
plt.xlabel("Trading days 13/05/2005-13/05/2015")
plt.show()
revealing the following picture:
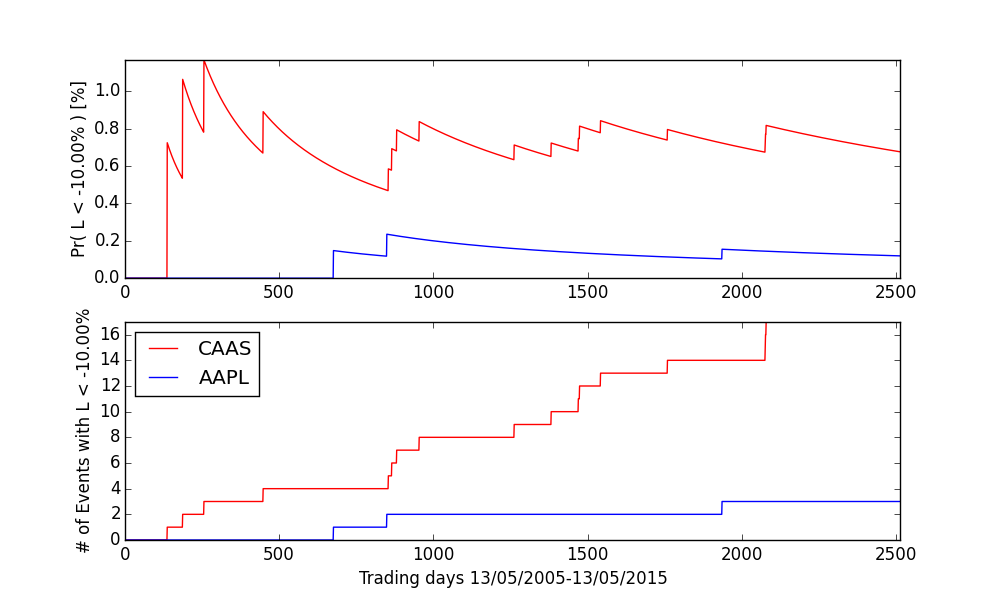
It’s a great way of looking at and understanding the far left-tail volatility of the asset under your current investigation. The probability between two rare/extreme events decreases for the obvious reason: along the time axis we include more and more data therefore the return distribution evolves and shifts its mass to the right leaving left tail events less and less probable.
The question remains: if an asset has never experienced an extreme loss of given magnitute, the probability of such event, within our VaR framework, simply remains zero! For example, for losses $L \lt -20$%,

CAAS displays 2 extreme events while AAPL none! Therefore, our estimation of superbly rare daily loss of -20% (or more) for AAPL stock based on 10 years of data is zero or undefined or… completely unsound. Can we do better than this?
2. Classical Conditional Prediction for Rare Events
Let’s consider a case where we want to predict the probability of the asset/stock (CAAS; traded at NASDAQ exchange) falling down more than $-L$%. Previously we have achieved such estimation through the integration of its probability density function. An alternative way is via derivation of the conditional probability, i.e. that CAAS will lose more than $-L$% given that NASDAQ index drops more than $-L$% on the next day.
Formula? Well, Bayes’ formula. That all what we need:
$$
\mbox{Pr}(B|R) = \frac{ \mbox{Pr}(R|B)\ \mbox{Pr}(B) } { \mbox{Pr}(R) } .
$$
Great, now, the meaning of each term. Let $A$ denotes the event of the stock daily return to be between -L% and 0%. Let B is the event of the stock return to be $\lt -L$%. Let $R$ is the event of NASDAQ daily return to be $\lt -L$%. Given that, based on both CAAS and NASDAQ historical time-series, we are able to compute $\mbox{Pr}(A)$, $\mbox{Pr}(B)$, $\mbox{Pr}(R|A)$, $\mbox{Pr}(R|B)$, therefore
$$
\mbox{Pr}(R) = \mbox{Pr}(R|A)\mbox{Pr}(A) + \mbox{Pr}(R|B)\mbox{Pr}(B)
$$ as well. Here, $\mbox{Pr}(R|A)$ would stand for the probability of NASDAQ falling down more than $-L$% given the observation of the CAAS return to be in $(-L;0)$% interval and $\mbox{Pr}(R|B)$ would denote the probability of NASDAQ falling down more than $-L$% given the observation of the CAAS return also dropping more than $-L$% on the same day.
With Bayes’ formula we inverse the engineering, aiming at providing the answer on $\mbox{Pr}(B|R)$ given all available data. Ready to code it? Awesome. Here we go:
# Predicting Heavy and Extreme Losses in Real-Time for Portfolio Holders
# (c) 2015 QuantAtRisk.com, by Pawel Lachowicz
#
# heavy2.py
import pandas.io.data as web
import matplotlib.pyplot as plt
import numpy as np
# ---1. Data Processing
# fetch and download daily adjusted-close price series for CAAS stock
# and NASDAQ index using Yahoo! Finance public data provider
'''
caas = web.DataReader("CAAS", data_source='yahoo',
start='2005-05-13', end='2015-05-13')['Adj Close']
nasdaq = web.DataReader("^IXIC", data_source='yahoo',
start='2005-05-13', end='2015-05-13')['Adj Close']
CAAScp = np.array(caas.values)
NASDAQcp = np.array(nasdaq.values)
f = file("data2.dat","wb")
np.save(f,CAAScp)
np.save(f,NASDAQcp)
f.close()
'''
f = file("data2.dat","rb")
CAAScp = np.load(f)
NASDAQcp = np.load(f)
f.close()
# compute the return-series
retCAAS = CAAScp[1:]/CAAScp[:-1]-1
retNASDAQ = NASDAQcp[1:]/NASDAQcp[:-1]-1
The same code as used in Section 1 but instead of AAPL data, we fetch NASDAQ index daily close prices. Let’s plot the return-series:
# plotting (figure #1)
# return-series for CAAS and NASDAQ index
#
plt.figure(num=2, figsize=(10, 6))
plt.subplot(211)
plt.grid(True)
plt.plot(retCAAS, '-r', label="CAAS")
plt.axis("tight")
plt.ylim([-0.25,0.5])
plt.legend(loc="upper right")
plt.ylabel("CAAS daily returns")
plt.subplot(212)
plt.grid(True)
plt.plot(retNASDAQ, '-', label="NASDAQ")
plt.legend(loc="upper right")
plt.axis("tight")
plt.ylim([-0.10,0.15])
plt.ylabel("NASDAQ daily returns")
plt.xlabel("Trading days 13/05/2005-13/05/2015")
plt.show()
i.e.,

where we observe a different trading dynamics for NASDAQ index between 750th and 1000th day (as counted from May/13, 2005). Interestingly, the heaviest losses of NASDAQ are not ideally correlated with those of CAAS. That make this case study more exciting! Please also note that CAAS is not the part of the NASDAQ index (i.e., its component). Bayes’ formula is designed around independent events and, within a fair approximation, we may think of CAAS as an asset ticking off that box here.
What remains and takes a lot of caution is the code that “looks at” the data in a desired way. Here is its final form:
# ---2. Computations of Conditional Probabilities for Rare Events
# isolate return-series displaying negative returns solely
# set 1 for time stamps corresponding to positive returns
nretCAAS = np.where(retCAAS < 0, retCAAS, 1)
nretNASDAQ = np.where(retNASDAQ < 0, retNASDAQ, 1)
# set threshold for rare events
thr = -0.065
# compute the sets of events
A = np.where(nretCAAS < 0, nretCAAS, 1)
A = np.where(A >= thr, A, 1)
B = np.where(nretCAAS < thr, retCAAS, 1)
R = np.where(nretNASDAQ < thr, retNASDAQ, 1)
nA = float(len(A[A != 1]))
nB = float(len(B[B != 1]))
n = float(len(nretCAAS[nretCAAS != 1])) # n must equal to nA + nB
# (optional)
print(nA, nB, n == (nA + nB)) # check, if True then proceed further
print(len(A), len(B), len(R))
print
# compute the probabilities
pA = nA/n
pB = nB/n
# compute the conditional probabilities
pRA = np.sum(np.where(R+A < 0, 1, 0))/n
pRB = np.sum(np.where(R+B < 0, 1, 0))/n
pR = pRA*pA + pRB*pB
# display results
print("Pr(A)\t = %5.5f%%" % (pA*100.))
print("Pr(B)\t = %5.5f%%" % (pB*100.))
print("Pr(R|A)\t = %5.5f%%" % (pRA*100.))
print("Pr(R|B)\t = %5.5f%%" % (pRB*100.))
print("Pr(R)\t = %5.5f%%" % (pR*100.))
if(pR>0):
pBR = pRB*pB/pR
print("\nPr(B|R)\t = %5.5f%%" % (pBR*100.))
else:
print("\nPr(B|R) impossible to be determined. Pr(R)=0.")
Python’s NumPy library helps us in a tremendous way by its smartly designed function of where which we employ in lines #69-72 and #86-87. First we test a logical condition, if it’s evaluated to True we grab the right data (actual returns), else we return 1. That opens for us a couple of shortcuts in finding the number of specific events and making sure we are still on the right side of the force (lines #73-79).
As you can see, in line #66 we specified our threshold level of $L = -6.5$%. Given that, we derive the probabilities:
(1216.0, 88.0, True) (2516, 2516, 2516) Pr(A) = 93.25153% Pr(B) = 6.74847% Pr(R|A) = 0.07669% Pr(R|B) = 0.15337% Pr(R) = 0.08186% Pr(B|R) = 12.64368%
The level of -6.5% is pretty random but delivers an interesting founding. Namely, based on 10 years of data there is 12.6% of chances that on May/14 2015 CAAS will lose more than -6.5% if NASDAQ drops by the same amount. How much exactly? We don’t know. It’s not certain. Only probable in 12.6%.
The outcome of $\mbox{Pr}(R|B)$ which is close to zero may support our assumption that CAAS has a negligible “influence” on NASDAQ itself. On the other side of the rainbow, it’s much more difficult to interpret $\mbox{Pr}(R)$, the probability of an “isolated” rare event (i.e., $L<-6.5$%) since its estimation is solely based on two players in the game: CAAS and NASDAQ. However, when computed for $N\ge 100$ stocks outside the NASDAQ index but traded at NASDAQ, such distribution of $\mbox{Pr}(R)$'s would be of great value as an another alternative estimator for rare events (I should write about it a distinct post).
Now, back the business. There is one problem with our conditional estimation of rare event probabilities as outlined within this Section. A quick check for $L = -10$% reveals:
[code lang="plain" gutter="false"]
Pr(A) = 98.69632%
Pr(B) = 1.30368%
Pr(R|A) = 0.00000%
Pr(R|B) = 0.00000%
Pr(R) = 0.00000%
Pr(B|R) impossible to be determined. Pr(R)=0.
[/code]
Let's remind that $R$ is the event of NASDAQ daily return to be $\lt -L$%. A quick look at NASDAQ return-series tells us the whole story in order to address the following questions that come to your mind: why, why, why zero? Well, simply because there was no event in past 10 year history of the index that it slid more than -10%. And we are cooked in the water.
A visual representation of that problem can be obtained by executing the following piece of code:
[code lang="python" firstline="104"]
from pyvar import cpr # non-at-all PEP8 style ;)
prob = []
for t in range(2,len(retCAAS)-1):
ret1 = retCAAS[0:t]
ret2 = retNASDAQ[0:t]
pBR, _ = cpr(ret1, ret2, thr=thr)
prob.append(pBR)
# plotting (figure #2)
# the conditional probability for rare events given threshold
#
plt.figure(num=2, figsize=(10, 6))
plt.plot(np.array(prob)*100., 'r')
plt.ylabel("Pr(B|R) [%%]")
plt.axis('tight')
plt.title("L$_{thr}$ = %.2f%%" % (thr*100.))
plt.xlabel("Trading days 13/05/2005-13/05/2015")
plt.show()
[/code]
where we moved all Bayes'-based calculations (lines #58-102) into a function cpr (a part of pyvar.py local library; see Download section below) and repeated our previous experiment, however, this time, $\mbox{Pr}(R|B)$ changing in time given the threshold of $L=-6.5$%. The resulting plot would be:

Before ca. 800th day the NASDAQ index was lacking any event of $L\lt -6.5$% therefore the $\mbox{Pr}(R|B)$ could not be determined. After that period we got some heavy hits and the conditional probability could be derived. The end value (as for May 13, 2015) is 12.64%.
Hope amongst Hopelessness?
There is no better title to summarise the outcomes we derived. Our goal was to come up with some (running) probability for very rare event(s) that, in our case, would be expressed as a 1-day loss of $-L$% in trading for a specified financial asset. In the first attempt we engaged VaR-related framework and the estimation of occurrence of the rare event based on the PDF integration. In our second attempt we sought for an alternative solution making use of Bayes’ conditional prediction of the asset’s loss of $-L$% (or more) given the observation of the same event somewhere else (NASDAQ index). For the former we ended up the a running probability of $\mbox{Pr}(L \le L_{thr})$ while for the latter with $\mbox{Pr}(R|B)$ given $L_{thr}$ for both B and R events.
Assuming $L_{thr}$ to be equal to -6.5%, we can present the corresponding computations in the following chart:

Well, the situation looks hopeless. It ain’t get better even if, as discussed earlier, the probability of $\mbox{Pr}(R)$ has been added. Both methodologies seem to deliver the answer to the same question however, somehow, we are left confused, disappointed, misled, in tasteless despair…
Stay tuned as in Part 2 we will see the light at the end of the tunnel. I promise.