The magnitude and importance of random numbers in finance does not have to be explained. We need them. Either it is an option pricing or a Monte Carlo simulation, random numbers are with us. However, we make a trade-off: the speed in their generation versus uniqueness. That is why a widely accepted use of, inter alia, Mersenne Twister algorithm as a source of pseudo-random numbers has established its position as a leading PRNG.
Contrary to that, the use of true random numbers in finance is not so direct and obvious. We obtain truly unique randomness but at the expense of speed. Additionally, the (re)sources are limited what makes highly repetitive tasks hard to accomplish in a reasonable time. As discussed in my book on True Random Number Generators (TRNGs), the hardware solutions might be an appealing alternative. But they are expensive. The choice is yours.
If TRNs are so difficult to fetch, do we need them for financial applications? Interestingly, the answer nowadays seems to be: Yes, we do.
With a dawn of new technology of blockchain emerging as an upcoming breakthrough for the world we know today, the application of true randomness for the needs of cryptographic protocols, security, addresses, and all underlying infrastructure (see more, e.g. the fundamentals of Bitcoin) constitutes a solid building block. Inevitable. Unbreakable. And in cryptography, within blockchain, we put our trust.
Let me refer your curiosity to my next book Cryptocurrencies and Crypto-Derivatives with Python upcoming in January 2017 but dive today into the practical aspect of blockchain mining: hacking a random sequence. As explained by Shirriff (2014), the mining requires a task that is very difficult to perform, but easy to verify. Bitcoin mining uses cryptography, with a hash function called double SHA-256. A hash takes a chunk of data as input and shrinks it down into a smaller hash value (in this case 256 bits). With a cryptographic hash, there’s no way to get a hash value you want without trying a whole lot of inputs. But once you find an input that gives the value you want, it’s easy for anyone to verify the hash. Thus, cryptographic hashing becomes a good way to implement the Bitcoin “proof-of-work”.
There two aspects in the process worth analysing: (1) generating a random (e.g. 64 char long) sequence of the highest cryptographic security (e.g. a public key); and (2) hacking it. In order to illustrate the problem of computational complexity with the use of a single CPU (of your PC) to perform those tasks (therefore to justify the use of dedicated hardware blockchain miners), let’s run a few lines of Python code. Below.
1. True Randomness in Python
Historically, the most trusted source of true random numbers has been established by Random.org website generating randomness from the atmospheric noise. The service allows for the URL-based calls for random alphanumeric sequences (e.g. used to create true-random passwords). Let’s fetch for 64-char random string first:
# Hacking True Random Numbers in Python: Blockchain Miners
# (c) 2016 QuantAtRisk.com
# ver Python 3.5
from urllib import request
import string
import numpy as np
import random
from time import time
from multiprocessing import Pool
from matplotlib import pyplot as plt
grey = .7, .7, .7
# fetch random sequence of len = n from Random.org composed of
# alphanumerics (0-9, a-z, A-Z)
t = time()
seq = []
for n in [20, 20, 20, 4]: # max length of n in one call is 20
url = "https://www.random.org/strings/?num=1&len=" + str(n) + \
"&digits=on&upperalpha=on&loweralpha=on&unique=on&format=" \
"plain&rnd=new"
response = request.urlopen(url)
raw = response.read().decode('utf8') # a raw sequence
seq.append(raw[0:n])
t = time() - t
seq = "".join(seq)
print("sequence '%s'\ngenerated in %.2f sec" % (seq, t))
sequence 'ySMOoGQ7Q0E5wT7sHSMuviofspBtzYcpKQ8hSO1EjEZ0HtiHcOc35a0gnvbUULjZ' generated in 3.85 sec
Atmospheric noise vouchsafes us a cryptographic security however the total time of getting the sequence from Random.org counts in seconds. In the Blockchain terminology, such long secure strings are referred to as hashes. Every operation of mining of a new block in the ledger requires “guessing” the hash in connection to information from the previous block. Hacking the hash requires enormous computer power to accomplish it in few minutes. To understand how difficult that task is, consider the a random string of length $n=3$ only, say:
seq = "2A7"
Now, let’s design a function which randomly (based on pseudo-random engine of Mersenne Twister built-in Python’s Standard Library) generates an alphanumeric string (composed of 0-9 digits, a-z and A-Z chars solely)
def str_generator(size=3, chars=string.ascii_uppercase + \
string.ascii_lowercase + string.digits):
return ''.join(random.choice(chars) for _ in range(size))
By running a simple Monte-Carlo simulation nsim times we examine the distribution of hacking time required to hack the 3-char long sequence of seq, i.e.:
# Monte-Carlo simulation
#
n = len(seq)
nsim = 1000 # number of simulations
res = []
t0 = time()
for _ in range(nsim):
out = str_generator(size=n)
t = time()
while(out != seq):
out = str_generator(size=n)
t = time() - t
#print("%10.2f %s %s" % (t,out, seq))
res.append(t)
print("%.2f sec per %g simulations" % (time()-t0, nsim))
print("\nmean = %.2f sec\nmedian = %.2f sec" % (np.mean(res),np.median(res)))
plt.figure(figsize=(7,3))
plt.hist(res, bins=50, color=grey, edgecolor=grey)
plt.xlabel("Hacking Time [sec]")
plt.ylabel("N")
returning
658.02 sec per 1000 simulations mean = 0.66 sec median = 0.44 sec
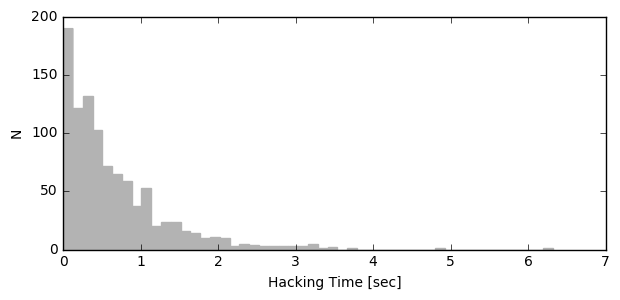
An attempt in hacking 4-char string requires a median time of 31-34 seconds whereas for 5-char string it is over 10 minutes (based on 4GHz Intel Core i7 CPU with running 1 core). The situation is not getting better if we try to employ all available CPU cores via multiprocessing library:
seq = "2A7"
n = len(seq)
out = str_generator(size=n)
nsim = 1000
res2 = []
pool = Pool()
pool.close()
pool.join()
for j in range(nsim):
t = time()
while True:
pool = Pool()
data_inputs = [n]*100000
out = pool.map(str_generator, data_inputs)
pool.close()
pool.join()
if(seq in out):
t = time() - t
res2.append(t)
#print(j, t)
break
print("mean = %.2f sec\nmedian = %.2f sec" %
(np.mean(res2), np.median(res2)))
cutting the time approximately by half:
mean = 0.36 sec median = 0.25 sec
2. Mining the Block
Going back to blockchain mining, hacking real hashes (64 bit) is analogous. Here is a slightly modified version of Shirriff’s (2014) code for the case study of an exemplary Bitcoin transaction discussed therein. By the application of randomised arrays of nonces, the probability of hacking the hash increases as a function of required time to complete the task:
# Src: http://www.righto.com/2014/02/bitcoin-mining-hard-way-algorithms.html
# tested with Python 2.7.10
import hashlib, struct
import numpy as np
from time import time
ver = 2
prev_block = "000000000000000117c80378b8da0e33559b5997f2ad55e2f7d18ec1975b9717"
mrkl_root = "871714dcbae6c8193a2bb9b2a69fe1c0440399f38d94b3a0f1b447275a29978a"
time_ = 0x53058b35 # 2014-02-20 04:57:25
bits = 0x19015f53
exp = bits >> 24
mant = bits & 0xffffff
target_hexstr = '%064x' % (mant * (1<<(8*(exp - 3))))
target_str = target_hexstr.decode('hex')
maxiter = 0x10000000 # trimmed; initially 0x100000000
print("maxiter = %.0f" % maxiter)
A = np.arange(maxiter)
A = np.random.choice(A, len(A), replace=False)
t = time()
for nonce in A[0:10000]: # use A[:] to go over maxiter
header = ( struct.pack("<L", ver) + prev_block.decode('hex')[::-1] +
mrkl_root.decode('hex')[::-1] + struct.pack("<LLL", time_, bits, nonce))
hash = hashlib.sha256(hashlib.sha256(header).digest()).digest()
if hash[::-1] < target_str:
print('success!')
print(nonce, hash[::-1].encode('hex'))
break
print("Computing power: %g hashes/sec" % (10000/(time()-t)))
maxiter = 268435456 Computing power: 172709 hashes/sec
Here we have tested a subsample of a large number of possible random combinations (dictated by the “current” complexity) to find the winning nonce:
success! 856192328 0000000000000000e067a478024addfecdc93628978aa52d91fabd4292982a50
Running the code and discovering its hacking time on your PC, I leave it with you as a homework.
It is now clear to understand the use of dedicated supercomputing powers to hack the hashes (the magnitude of TH/s; Tera hashes/sec), achieve consensus across the blockchain ledger, and mine a new block.
Truly random. Truly breathtaking.
REFERENCES
Lachowicz P., 2017, Blockchain Quantitative Finance: Introduction to Technology
and Data Analysis (upcoming post)
Shirriff B., 2014, Bitcoin mining the hard way: the algorithms, protocols, and bytes