In Financial Risk Management the most challenging part for quantitative modeling is, beyond any doubt, the Operational Risk (Ops Risk). It is defined as the risk of loss resulting from inadequate or failed internal processes, people and systems or from external events. This definition includes legal risk, but excludes strategic and reputation risk. According to Basel Committee, (not only American) banks are encouraged to move along the spectrum of available approaches as they develop more sophisticated operational risk measurement systems and practices.
For every bank or other financial institution a design of the inner system that captures correctly all events of being “operational” in nature and causing an institution to lose money is of paramount importance. For example, banks cannot allow themselves for “one-day off” from their transactional activities due to an IT system breakdown or a power shortage which prevents the bank’s building from its normal daily operations. The list of things that might go wrong is long. The bottom line is that everyone needs to monitor, record, and prevent “the next big thing” (i.e. a loss) due to Ops Risk event.
The quantitative modeling of operational risk additionally is difficult due to the lack of rich data on the past events. Even if they internally exist in a form of a decent database, the number of events per period of time is often very low. The less data we have the worst prediction for the future we can make.
Aside from pure forecasting of the numbers of Ops Risk events for a whole financial institution and associated with them loss distribution, a detailed picture is usually required. In general, say, a bank is composed of $N$ lines of business (LOB) which operate daily and their performance (including Ops Risk losses) is monitored and reviewed monthly or quarterly. Each LOB, for example Asset Servicing or Broker Dealer Services, has different characteristics and profile. Among $N$ LOB, one line may “generate” a very small number of Ops Risk losses but of million dollar magnitudes. The other one can be characterized by 15 to 35 Ops Risk events per quarter with the overall small dollar losses.
The risk managers not only seek for the ways to mitigate and limit the overall operational risk losses to the absolute minimum on the quarter-to-quarter basis but also need a tool to allocate properly the operational risk capital charges per LOB. By Ops Risk capital charges one may understand the dollar amount of money the bank should allocate for a specific LOB for the upcoming period of time to cover all potential Ops Risk losses. The problem of allocation is highly challenging itself. On one side, the bank (i.e. the brightest quants working in the bank) try to analyze LOB and its Ops Risk profile the best way they can. That allows them to model and forecast the overall severity of LOB. Given that, usually a Monte Carlo approach is applied in order to allocate a “right” amount of capital charges per LOB. “Right” is a crucial word here. A classical method employing simulation is mainly based on the analysis of the past records and assumption that the future will follow the same trend. It occurs that such Monte Carlo-based allocations tend to overestimate the LOB-specific capital charges. Is it a bad news for the bank? On one hand no as the higher Ops Risk capital charges the more money banks keeps aside to cover the losses. On the other hand, yes because the bank, on average, keeps too much aside and we know very well that the money kept in the pocket do not earn any interest!
That long story written short brings us to the concept of fair allocation of money among $N$ players of the game. And a term “game” occurs here for a reason.
1. Shapley Value
The allocation of Ops Risk capital charges is analogous to the allocation of risk (levels) to individual LOB. The sum of the risks incurred by each LOB in isolation does not equal the total risk for the bank. That complicates the picture. Simple summation ignores that interactions among individual LOB could reduce or compound overall risk. They would reduce it when position across LOB partially cancel each other out and they would compound it when losses in one side of the business are incurred simultaneously with (or trigger) losses in another (Tarashev, Borio, and Tsatsaronis 2009).
Mathematicians have been bothered by similar problems in the context of cooperative games. These are general settings where a group of players engage in a collective effort in order to generate a shared benefit (i.e. value) for the group. The theoretical problem of allocating this value among individual players in a way that satisfies certain fundamental criteria is conceptually identical to that of risk attribution among $N$ LOB.
In 1953 Lloyd Shapley proposed a methodology that distributes the overall value among players on the basis of their individual contributions. The idea behind the allocation methodology is quite simple. Adding up what individual players can achieve by themselves is unlikely to reflect their contributions to the productivity of others. Similarly, calculating the marginal contribution of a single player as the difference between what the entire group can achieve with and without the specific individual gives only a partial picture of the individual’s contribution to the work of others. The reason is that this method also ignores the complexities of bilateral relationships. By contrast, the Shapley Value methodology accounts fully for the degree to which such relationships affect the overall outcome. It accomplishes this by ascribing to individual players the average marginal contribution each makes to each possible subgroup in which they participate.
Shapley allocation method incorporates the concept of diversification in its premises such that capital is allocated in a way that the managers of business units can consider as fair. Shapley’s achievement showing that there was a single optimal (i.e. ‘fairest’) allocation solution led him to receiving the 2012 Nobel Prize for Economics.
Shapley allocation is, in principal, a ‘fair’ allocation method because it accounts for the benefits of forming coalitions. In our understanding, we would consider a ‘coalition’ of a few LOB as a joint contribution of these LOB to the bank’s riskiness due to incurred Ops Risk losses. One may define the Grand Coalition (GC) as a coalition composed of $N$ LOB (a portfolio) and any permutation of LOB forming (a simple) coalition $s$. In this way, every coalition (also GC) would have its value, $\nu(\cdot)$, and being formed by $n$ members.
Therefore, adopted to the operational risk framework, the Shapley’s original allocation formula would provide the allocation of an $i$-th LOB’s Ops Risk capital charges, in a coalition $C$, as:
\begin{equation}
\varphi_i = \sum_{i\in C} \frac{s!(n-s-1)!}{n!} \left[ \nu(s) – \nu(s-\{i\}) \right]
\end{equation}
where the term $[\nu(s) – \nu(s-\{i\})]/n!$ represents the mean of the marginal values added when $i$-th LC joins coalition $s$ and the function $\nu$ is called a characteristic function (see more here).
In practical applications one uses a computer algorithm to obtain Shapley value for each contributor. It considers all available permutations of players and for each permutation the mean value of the marginal effect of a new LOB to the existing coalition is examined. Therefore, one can describe the Shapley value as the mean value of the marginal contributions for each LOB.
Let’s consider 10 LOB for a certain bank and their total annual Ops Risk losses as captured by the following R code:
# Shapley Value Allocaiton of N-LOB Ops Risk
#
# (c) 2018 QuantAtRisk.com
# by Pawel Lachowicz
# R-Studio setup
while (dev.cur()>1) dev.off() # close all windows
rm(list=ls(all=TRUE)) # clean memory
cat("\014") # clear console
options(warn=-1) # warnings off, on =0
options(max.print=999999)
# load required R libraries
require("combinat")
require("GameTheoryAllocation")
# N-LOB Portfolio (Ops Risk annual losses)
L = c( 2345005, # LOB No.1
3450095, # LOB No.2
3904723, # ...
4500905,
5004813,
5390230,
7209302,
8397000,
8394003,
10203200) # LOB No.10
Na = length(L)
a = c(1:Na)
We can see that, in a sorted order, the LOB-specific incurred losses were between 2.34M and 10.2M USD with the total Ops Risk loss of 58.8M USD at the bank level.
Under earlier assumption about the future to be about the same as the past, one can consider a fair (Shapley) allocation of Ops Risk capital charges for all ten LOB by deriving, first, the characteristic function:
# characteristic funciton (charfun)
for(n in 1:Na){
x = DescTools::CombSet(a, n, repl = FALSE)
xr = dim(x)[1]
xc = dim(x)[2]
flat = as.numeric(x)
flat = L[flat]
unflat = matrix(flat, nrow = xr, ncol = xc, byrow = FALSE)
if(n == 1){
charfun = apply(unflat,1,max)
}else{
charfun = c(charfun, apply(unflat,1,max))
}
}
names(charfun) = NULL
charfun = (charfun[1:length(charfun)])
k = length(charfun)
and next the Shapley value allocation:
t0 = Sys.time() ShapleyValue = c(Shapley_value(charfun, game="cost")) print(difftime(Sys.time(), t0, units="mins")) cbind(L, ShapleyValue) colSums(cbind(L, ShapleyValue))
to return the following output numbers:
L ShapleyValue
[1,] 2,345,005 50,559.18
[2,] 3,450,095 603,141.69
[3,] 3,904,723 664,709.63
[4,] 4,500,905 591,704.01
[5,] 5,004,813 839,743.03
[6,] 5,390,230 877,239.76
[7,] 7,209,302 1,240,955.99
[8,] 8,397,000 1,414,100.94
[9,] 8,394,003 1,646,527.15
[10,] 10,203,200 2,274,518.62
L ShapleyValue
58,799,276 10,203,200
The problem with this solution is that the sum over all Shapley allocations falls over five times below the total of all annual losses. Moreover, the sum is equal to the annual loss incurred by LOB No.10, exactly. Therefore, Shapley values allocation, in this version, splits “fairly” individual contributions among all ten LOB as if the grand total would be 10.2M USD high.
To understand this better let’s consider a classical problem of a “fair” split of a fare among three friends who share the same taxi (watch Knight 2012). Each one travels different distance to their homes and the one who lives at the furthest end of the city needs to pay for a whole taxi ride 42 USD. As they get in the cab, they decide to contribute as high as 6 USD (the first person to drop off) and 12 USD (the second person to drop off) to the total of 42 USD the last person needs to pay for a whole ride. In that case, the third person’s contribution to the fare would be 24 USD as he received 18 USD from his friends. Is it fair? Well, if we rerun the above code with:
L = c( 6, 12, 42)
we would find that a fair taxi fare split among three friends should be 2, 5, and 35 USD, respectively:
L ShapleyValue
[1,] 6 2
[2,] 12 5
[3,] 42 35
L ShapleyValue
60 42
This version of Shapley Value allocation approach is not exactly what we need to fairly allocate Ops Risk capital charges based on LOB annual losses. The main drawback is that it does not take into account the number of Ops Risk events. Luckily, this can be fixed by a smart observation of achievements following the original work of Shapley (1953).
2. Airport Problem: Shapley Value in a Special Case
In 1973 Littlechild & Owen published across Management Science a three-page note on a simple and easily calculated expression for the Shapley value. The inspiration came from some earlier work of Baker (1965) and Thompson (1971) on setting airport landing charges for different types of aircraft. Among game theorists this is known as an airport problem.
It was suggested that the cost of providing an airport runway essentially depended upon the largest type of aircraft to land there. If so, a simple rule for allocating these costs was as follows: divide the cost of catering for the smallest type of aircraft equally among the number of landings of all aircrafts; next, divide the incremental cost of catering for the second smallest type of aircraft (above the cost of the smallest type) equally among the number of landings of all but the largest type of aircraft; continue thus until finally the incremental cost of the largest type of aircraft (above the cost of the second largest type) is divided equally among the number of landings made by the largest aircraft type.
Littlechild & Owen saw an opportunity to provide an elegant solution to the airport problem by using a simplified expression for the Shapley value. The landing charges occurred to be exactly the Shapley value for an appropriately defined game whenever the characteristic function is a “cost” function with the property that the cost of any subset of players is equal to the cost of the “largest” player in that subset.
In particular, if we consider $n_i$ to be the number of landings of an aircraft type $i$ such that $i=1,…,N$ where $N$ is the total number of all aircraft types and
$$
n = \sum_{i=1}^N n_i \ ,
$$let $c_i$ be the “cost” associated with a player type $i$ (e.g. annual capital cost). We may order the aircraft types such that:
$$
0 = c_0 < c_1 < c_2 < ... < c_N
$$ If by $K_i$ we denote a set of players type $i$ and $K = \bigcup_{i=1}^N K_i$, we may define a game on $K$ by the subaddtive characteristic function:
$$
\nu(\emptyset) = 0, \ \ \ \nu(s) = \max\{ c_i \} \ ,
$$ where the maximisation is taken over all $i$ such that $K_i$. Now, if we take the Shapley value $\varphi_j$ for the game $(N,C)$ as:
$$
\varphi_j(\nu) = \sum_{i\in s; s\subseteq K} \frac{(n-s)!(s-1)!}{n!} \left[ \nu(s) - \nu(s-\{i\}) \right]
$$ then what Littlechild & Owen proposed was that the expression for the Shapley value could be simplified to:
$$
\varphi_j(\nu) = \sum_{k=1}^i \frac{c_k - c_{k-1}}{r_k} \ \ \mbox{for} \ \ j\in K_i, \ i=1,...,N \ .
$$ where $r_k$ was defined as
$$
r_k = \sum_{i=k}^N n_i \ \ \mbox{for} \ \ k = 1,...,N \ .
$$ It worth to note here that if $i=1$ then $\varphi_0 = 0$ and $c_0=0$. The calculations of Shapley value capital charges in the airport problem follow for $i=1$:
$$
\varphi_1 = c_1/r_1
$$ and for $i>1$:
$$
\varphi_i = \varphi_{i-1} + \frac{c_i – c_{i-1}}{N-i+1} \ .
$$ Given that, one can easily recreate the values of Shapley value capital charges presented by Littlechild & Owen in their example, i.e.
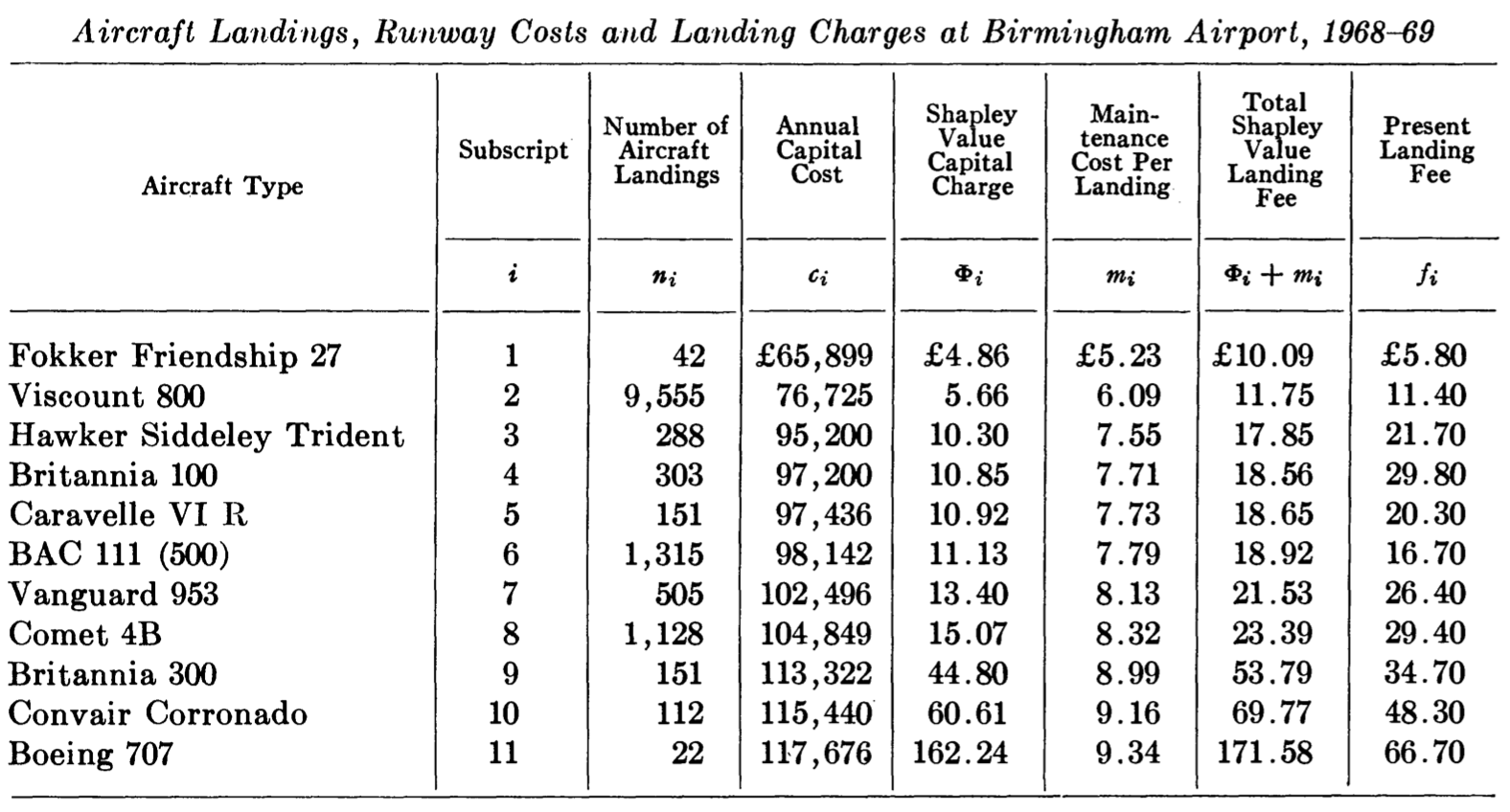
If we ignore a maintenance cost per landing, $m_i$, a sole Shapley values $\Phi_i$ in the Table build a “fair” structure of fees per landing for all aircraft types. Again, it is important to note that the above solution delivered by Littlechild & Owen takes into account not only the annual capital cost per aircraft type but also includes in calculations the number of aircraft landings in a year. The analogy to Ops Risk LOB capital charges is striking!
3. Allocation of Operational Risk Capital Charges using Airport Problem Solution
Operational risk losses can be summarised by the dollar amount of loss (aggregated) over a certain period of time and the frequency of loss events (here, the number of Ops Risk events). If the former we express by $c_i$ and the latter by $n_i$, respectively for $N$ LOB in the bank’s portfolio $(i=1,…,N)$ then using the solution of the airport problem one can find a “fair” allocation of the capital charge (dollar amount) per 1 Ops Risk event for each LOB.
Continuing our example of annual Ops Risk losses from the R code, by applying a new Shapley value expression, we find:
LOB No. of Events Annual Loss Original ShV Shapley Value (i) (n_i) (c_i) (r_k) (phi_i) 1 24 2,345,005 50,559.18 436 5,378 2 99 3,450,095 603,141.69 412 8,061 3 34 3,904,723 664,709.63 313 9,513 4 67 4,500,905 591,704.01 279 11,650 5 43 5,004,813 839,743.03 212 14,027 6 65 5,390,230 877,239.76 169 16,308 7 34 7,209,302 1,240,955.99 104 33,799 8 14 8,397,000 1,414,100.94 70 50,766 9 35 8,394,003 1,646,527.15 56 50,712 10 21 10,203,200 2,274,518.62 21 136,864 Total n = 436 58,799,276 10,203,200.00 337,078
where we added number of events per LOB $n_i$ in a year. The calculated new Shapley values, if multiplied by the corresponding $n_i$’s sum up to 10,203,200, i.e. to the annual loss of LOB No 10 as expected. However since the use of historical numbers of events as given above leads to underestimation of the aggregated capital charge, it is a wiser solution to consider the allocation based on estimated upper bound for the number of events, e.g.:
$$
\zeta = \bar{n} + 3\sigma
$$ If so, we obtain Shapley value allocation of Ops Capital Charges for 10-LOB portfolio:
LOB Shapley Allocation (i) (phi_i*zeta) 1 654,722.49 2 981,235.44 3 1,158,047.47 4 1,418,168.00 5 1,707,512.59 6 1,985,128.37 7 4,114,328.70 8 6,179,746.72 9 6,173,231.96 10 16,660,600.74 Total 41,032,722.48
Although the total of 41M USD is lower than a historical (latest) total loss incurred of 58.8M USD, the calculated charges, $\varphi_i\zeta$, can be treated as “fair” within this Shapley framework.